Vector Databases
A vector databases is a specialized type of database that plays an essential role in AI applications.
In vector databases, queries differ from traditional relational databases. Instead of exact matches, they perform similarity searches. When given a vector as a query, a vector database returns vectors that are “similar” to the query vector. Further details on how this similarity is calculated at a high-level is provided in a later section.
Vector databases are used to integrate your data with AI models. The first step in their usage is to load your data into a vector database. Then, when a user query is to be sent to the AI model, a set of similar documents is first retrieved. These documents then serve as the context for the user’s question and are sent to the AI model, along with the user’s query. This technique is known as Retrieval Augmented Generation (RAG).
The following sections describe the Spring AI interface for using multiple vector database implementations and some high-level sample usage.
The last section attempts to demystify the underlying approach of similarity searching in vector databases.
API Overview
This section serves as a guide to the VectorStore interface and its associated classes within the Spring AI framework.
Spring AI offers an abstracted API for interacting with vector databases through the VectorStore interface.
Here is the VectorStore interface definition:
public interface VectorStore {
void add(List<Document> documents);
Optional<Boolean> delete(List<String> idList);
List<Document> similaritySearch(String query);
List<Document> similaritySearch(SearchRequest request);
}and the related SearchRequest builder:
public class SearchRequest {
public final String query;
private int topK = 4;
private double similarityThreshold = SIMILARITY_THRESHOLD_ALL;
private Filter.Expression filterExpression;
public static SearchRequest query(String query) { return new SearchRequest(query); }
private SearchRequest(String query) { this.query = query; }
public SearchRequest withTopK(int topK) {...}
public SearchRequest withSimilarityThreshold(double threshold) {...}
public SearchRequest withSimilarityThresholdAll() {...}
public SearchRequest withFilterExpression(Filter.Expression expression) {...}
public SearchRequest withFilterExpression(String textExpression) {...}
public String getQuery() {...}
public int getTopK() {...}
public double getSimilarityThreshold() {...}
public Filter.Expression getFilterExpression() {...}
}To insert data into the vector database, encapsulate it within a Document object.
The Document class encapsulates content from a data source, such as a PDF or Word document, and includes text represented as a string.
It also contains metadata in the form of key-value pairs, including details such as the filename.
Upon insertion into the vector database, the text content is transformed into a numerical array, or a List<Double>, known as vector embeddings, using an embedding model. Embedding models, such as Word2Vec, GLoVE, and BERT, or OpenAI’s text-embedding-ada-002, are used to convert words, sentences, or paragraphs into these vector embeddings.
The vector database’s role is to store and facilitate similarity searches for these embeddings. It does not generate the embeddings itself. For creating vector embeddings, the EmbeddingClient should be utilized.
The similaritySearch methods in the interface allow for retrieving documents similar to a given query string. These methods can be fine-tuned by using the following parameters:
-
k: An integer that specifies the maximum number of similar documents to return. This is often referred to as a 'top K' search, or 'K nearest neighbors' (KNN). -
threshold: A double value ranging from 0 to 1, where values closer to 1 indicate higher similarity. By default, if you set a threshold of 0.75, for instance, only documents with a similarity above this value are returned. -
Filter.Expression: A class used for passing a fluent DSL (Domain-Specific Language) expression that functions similarly to a 'where' clause in SQL, but it applies exclusively to the metadata key-value pairs of aDocument. -
filterExpression: An external DSL based on ANTLR4 that accepts filter expressions as strings. For example, with metadata keys like country, year, andisActive, you could use an expression such as
country == 'UK' && year >= 2020 && isActive == true.Available Implementations
These are the available implementations of the VectorStore interface:
-
InMemoryVectorStoreandSimplePersistentVectorStore. -
Pinecone: PineCone vector store.
-
PgVector [
PgVectorStore]: The PostgreSQL/PGVector vector store. -
Milvus [
MilvusVectorStore]: The Milvus vector store -
Neo4j [
Neo4jVectorStore]: The Neo4j vector store -
Weaviate [
WeaviateVectorStore] The Weaviate vector store -
Azure Vector Search [
AzureVectorStore] the Azure vector store
More implementations may be supported in future releases.
If you have a vector database that needs to be supported by Spring AI, open an issue on GitHub or, even better, submit a pull request with an implementation.
Information on each of the Vector Store implementations can be found in the subsections of this chapter.
Example Usage
To compute the embeddings for a vector database, you need to pick an embedding model that matches the higher-level AI model being used.
For example, with OpenAI’s ChatGPT, we use the OpenAiEmbeddingClient and a model name of text-embedding-ada-002.
The Spring Boot starter’s auto-configuration for OpenAI makes an implementation of EmbeddingClient available in the Spring application context for dependency injection.
The general usage of loading data into a vector store is something you would do in a batch-like job, by first loading data into Spring AI’s Document class and then calling the save method.
Given a String reference to a source file that represents a JSON file with data we want to load into the vector database, we use Spring AI’s JsonReader to load specific fields in the JSON, which splits them up into small pieces and then passes those small pieces to the vector store implementation.
The VectorStore implementation computes the embeddings and stores the JSON and the embedding in the vector database:
@Autowired
VectorStore vectorStore;
void load(String sourceFile) {
JsonReader jsonReader = new JsonReader(new FileSystemResource(sourceFile),
"price", "name", "shortDescription", "description", "tags");
List<Document> documents = jsonReader.get();
this.vectorStore.add(documents);
}Later, when a user question is passed into the AI model, a similarity search is done to retrieve similar documents, which are then "'stuffed'" into the prompt as context for the user’s question.
String question = <question from user>
List<Document> similarDocuments = store.similaritySearch(question);Additional options can be passed into the similaritySearch method to define how many documents to retrieve and a threshold of the similarity search.
Metadata Filters
This section describes various filters that you can use against the results of a query.
Filter String
You can pass in an SQL-like filter expressions as a String to one of the similaritySearch overloads.
Consider the following examples:
-
"country == 'BG'" -
"genre == 'drama' && year >= 2020" -
"genre in ['comedy', 'documentary', 'drama']"
Filter.Expression
You can create an instance of Filter.Expression with a FilterExpressionBuilder that exposes a fluent API.
A simple example is as follows:
FilterExpressionBuilder b = new FilterExpressionBuilder();
Expression expression = b.eq("country", "BG").build();You can build up sophisticated expressions by using the following operators:
EQUALS: '=='
MINUS : '-'
PLUS: '+'
GT: '>'
GE: '>='
LT: '<'
LE: '<='
NE: '!='You can combine expressions by using the following operators:
AND: 'AND' | 'and' | '&&';
OR: 'OR' | 'or' | '||';Considering the following example:
Expression exp = b.and(b.eq("genre", "drama"), b.gte("year", 2020)).build();You can also use the following operators:
IN: 'IN' | 'in';
NIN: 'NIN' | 'nin';
NOT: 'NOT' | 'not';Consider the following example:
Expression exp = b.and(b.eq("genre", "drama"), b.gte("year", 2020)).build();Understanding Vectors
Vectors have dimensionality and a direction. For example, the following image depicts a two-dimensional vector in the cartesian coordinate system pictured as an arrow.

The head of the vector is at the point . The x coordinate value is and the y coordinate value is . The coordinates are also referred to as the components of the vector.
Similarity
Several mathematical formulas can be used to determine if two vectors are similar.
One of the most intuitive to visualize and understand is cosine similarity.
Consider the following images that show three sets of graphs:
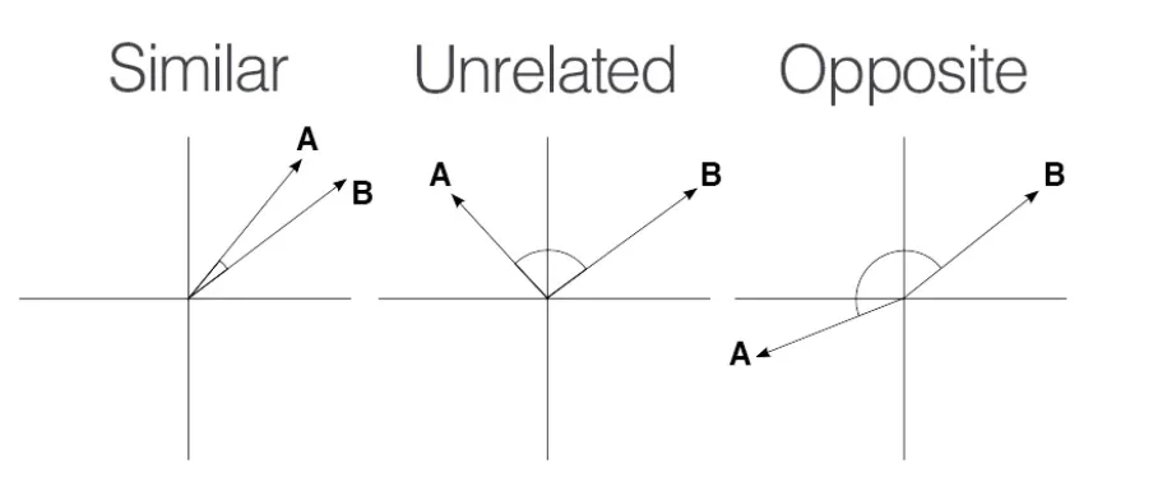
The vectors and are considered similar, when they are pointing close to each other, as in the first diagram. The vectors are considered unrelated when pointing perpendicular to each other and opposite when they point away from each other.
The angle between them, , is a good measure of their similarity. How can the angle be computed?
We are all familiar with the Pythagorean Theorem.
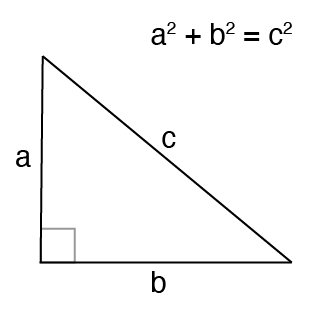
What about when the angle between a and b is not 90 degrees?
Enter the Law of cosines.
The following image shows this approach as a vector diagram:
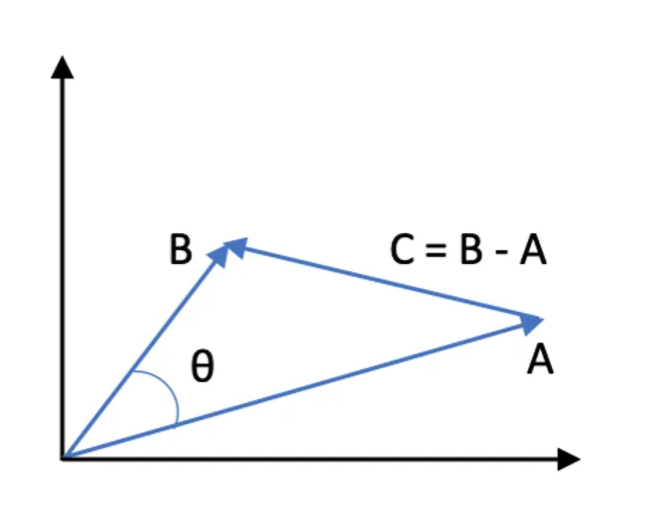
The magnitude of this vector is defined in terms of its components as:
The dot product between two vectors
Rewriting the Law of Cosines with vector magnitudes and dot products gives the following:
Replacing
Expanding this out gives us the formula for Cosine Similarity.
This formula works for dimensions higher than 2 or 3, though it is hard to visualize. However, it can be visualized to some extent. It is common for vectors in AI/ML applications to have hundreds or even thousands of dimensions.
The similarity function in higher dimensions using the components of the vector is shown below. It expands the two-dimensional definitions of Magnitude and Dot Product given previously to N dimensions by using Summation mathematical syntax.
This is the key formula used in the simple implementation of a vector store and can be found in the InMemoryVectorStore implementation.